Check out the paper on this new method and the code for optical interferometry of rotating, spotted stars.

Combining telescopes

Even if we look at the nearest star to the Sun with the biggest telescope in the world, we would see nothing but a ripple called an Airy disk, due to the wave nature of light. So astronomers rely on other techniques to map stars, usually less direct than taking a picture. The best and most direct of these is called interferometry, where you combine telescopes that are spaced far apart to get the resolving power of a huge telescope the size of the distance between the telescopes. It’s the closest you can get to taking a picture, even if it’s only been used a handful of times. But there are still gaps with interferometry. Each pair of telescopes gives you a single point on a Fourier transform (FT) at each moment in time, leaving large gaps in the frequency domain. We need to find a way to fill these gaps to invert the Fourier transform and get an image!

My approach

We can use our knowledge that our star has a spotty surface on a disk to reduce the number of solutions to our problem. If we know the star is rotating, we know the features on its surface will rotate along with it! In our paper, we use the spherical harmonics to represent the intensity on a star’s surface (figure from Luger et al. 2019:

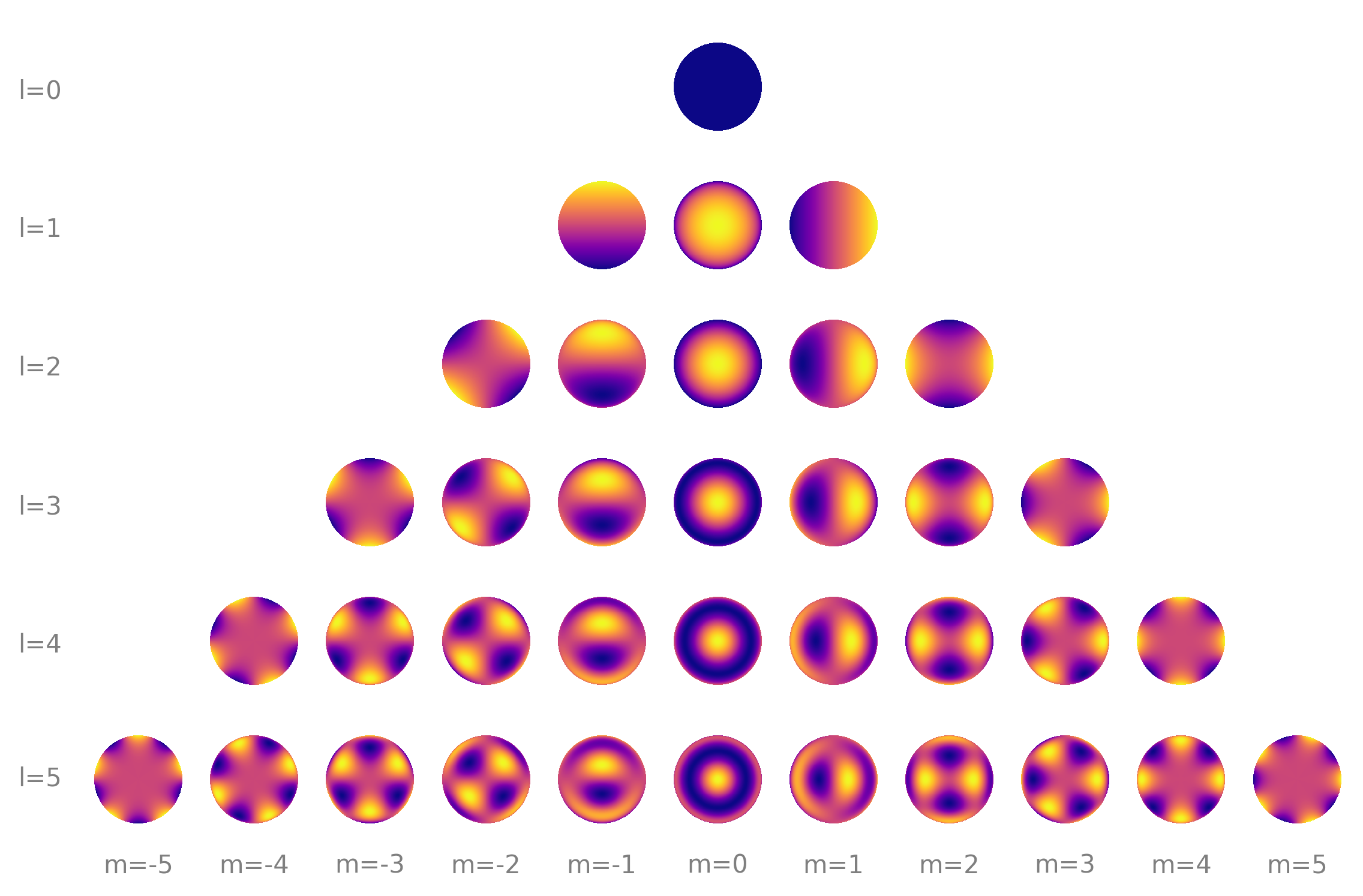
With the star’s map described in spherical harmonics, we found a really neat analytic solution to its Fourier transform. This gives us the visibility function, which is closely related to what we measure from an interferometer. And the solution is linear with respect to the star’s map!

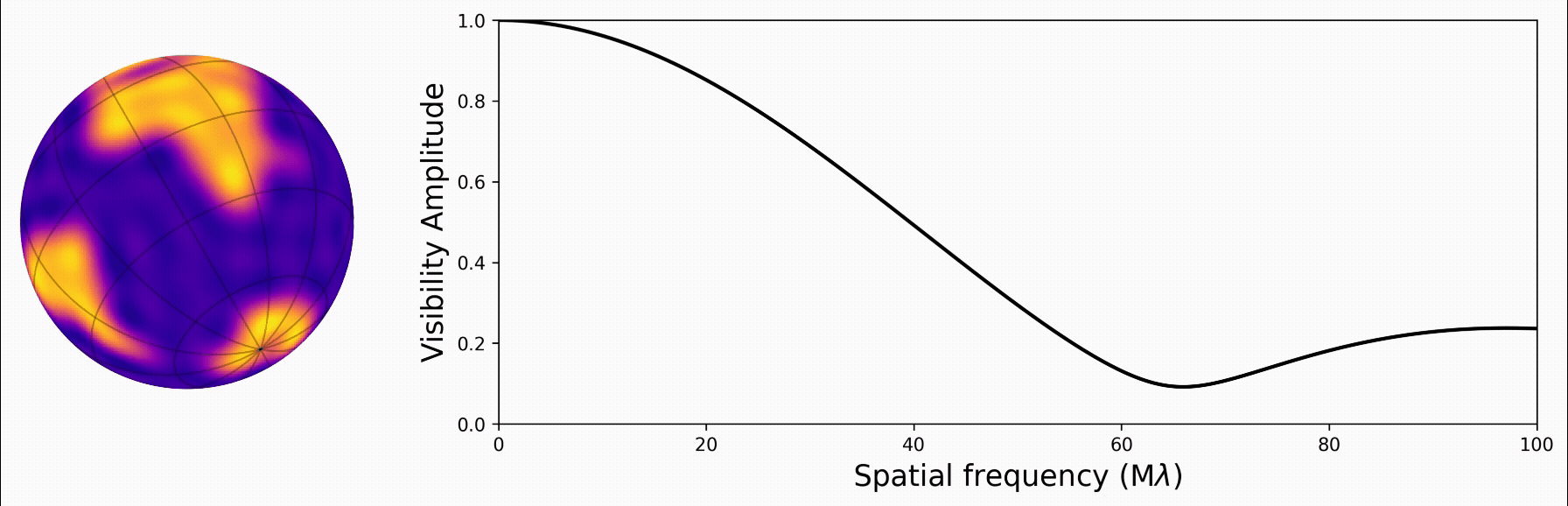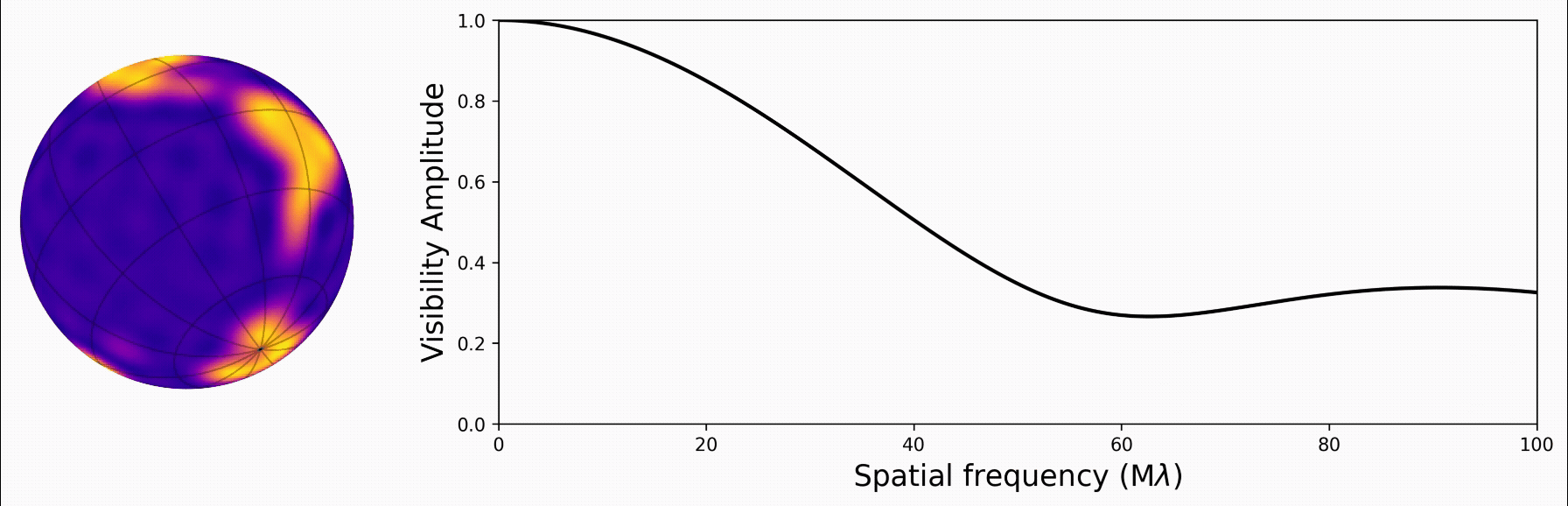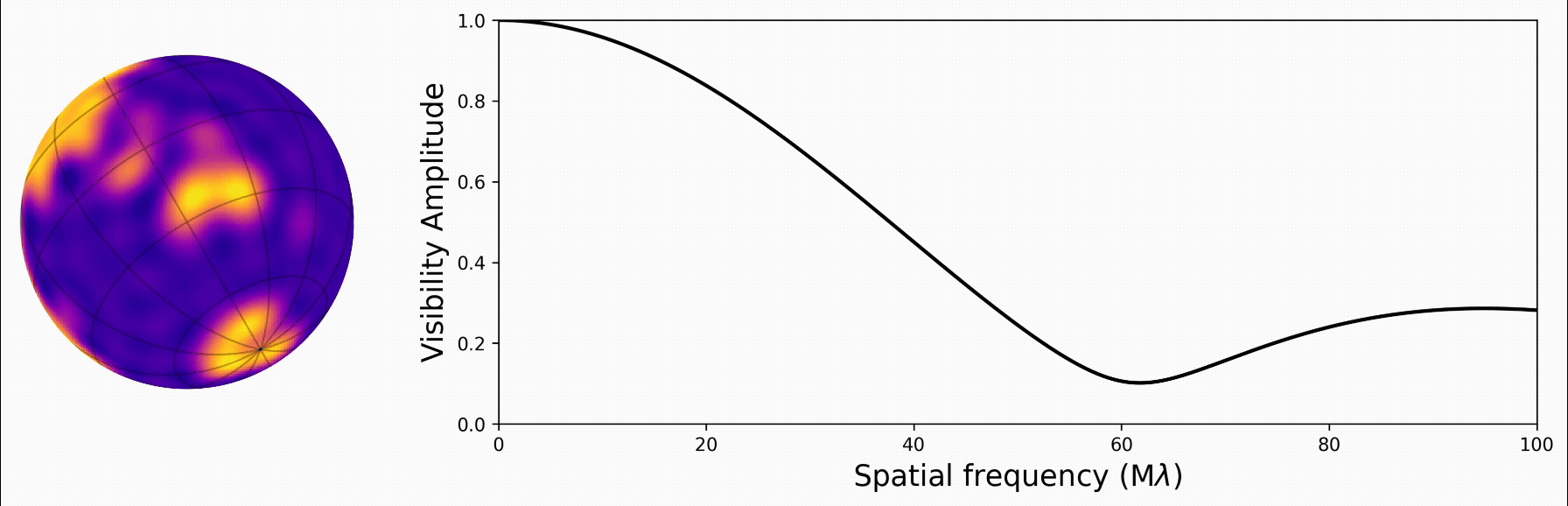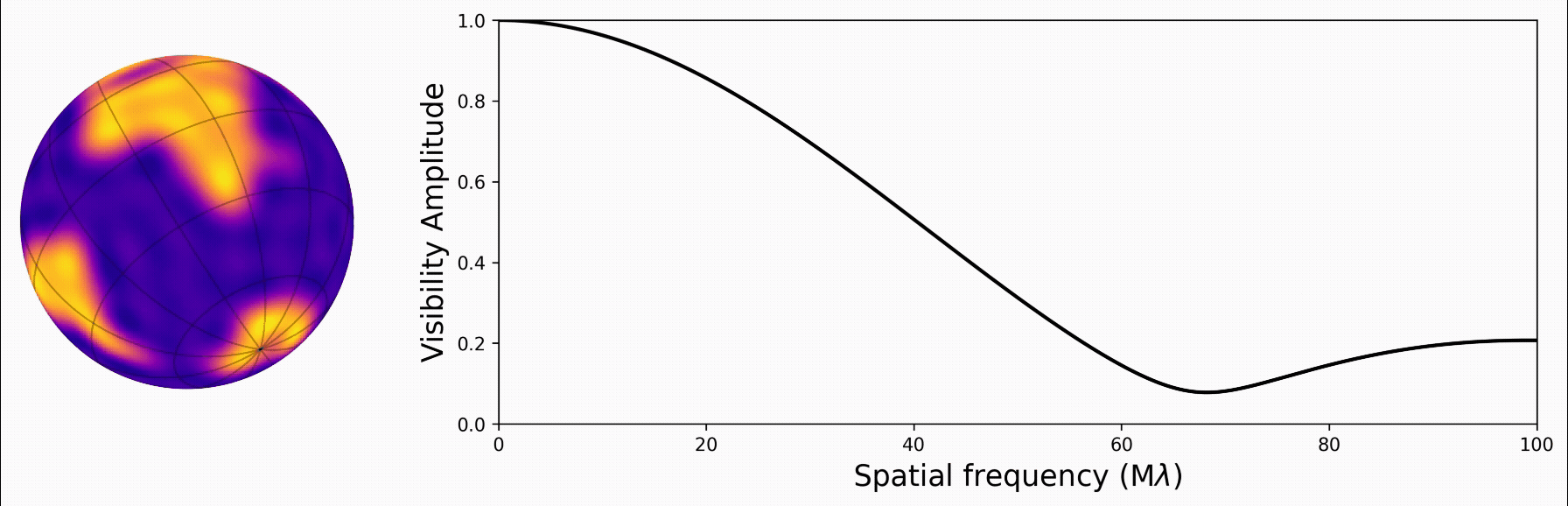
We implement this new math in a new Python/JAX package called harmonix, which is based on and designed to work with a suite of other JAX codes for mapping stars and planets.

The SPOT star

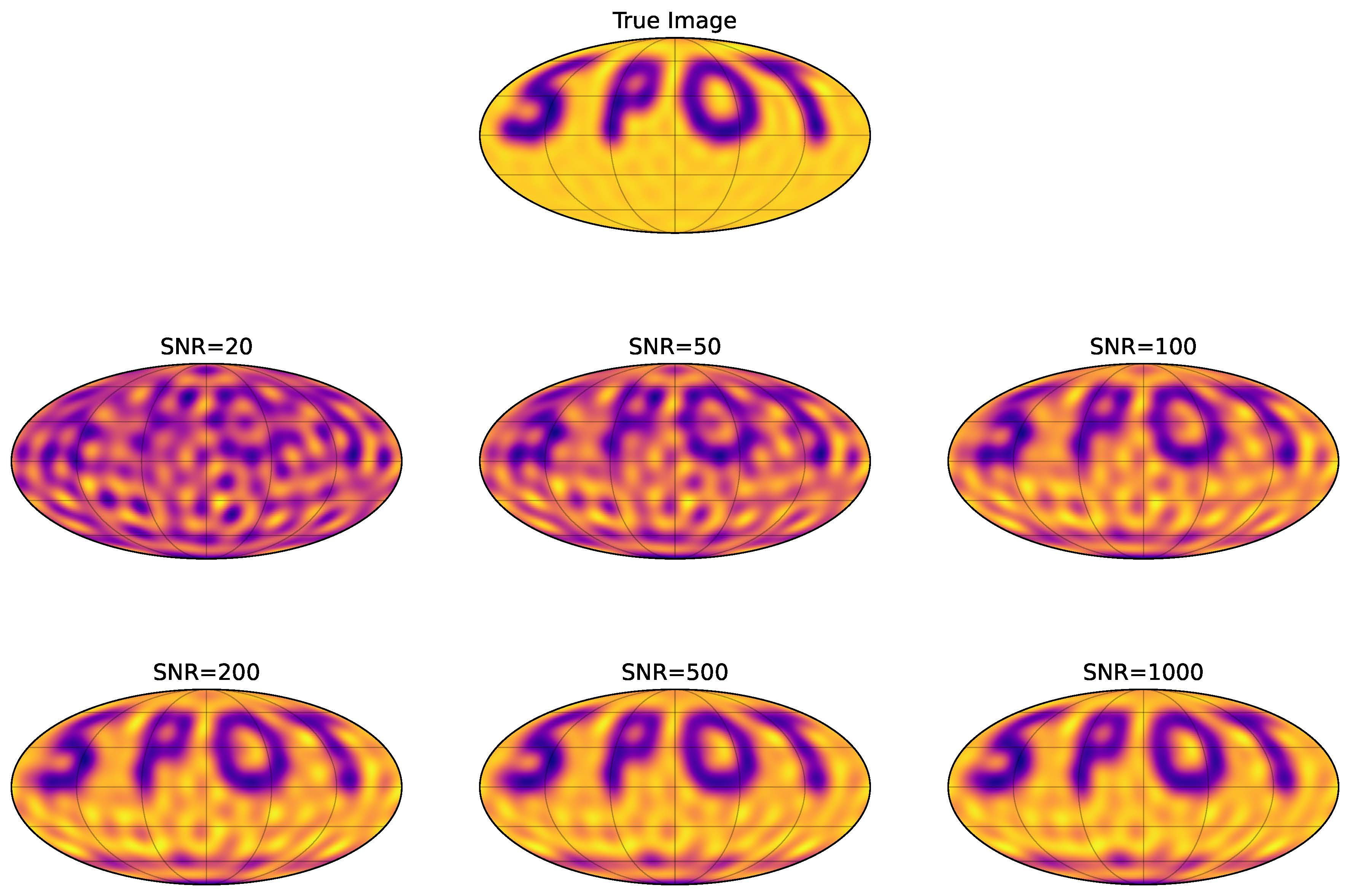
Armed with this new math and code, we set out to tackle a toy experiment first done for Doppler imaging spectroscopy by Vogt in 1987 but as far as I know, not tried for interferometry. Just like Luger et al. (2021), we paint a hypothetical star’s surface with the word ‘SPOT’. We then try to see if we can image this SPOT star using interferometry.

I simulate observing it with the CHARA Array and inject different levels of noise into the simulated data and optimize to find the best-fitting map. At high signal-to-noise we basically recover a perfect map!

Combining interferometry and photometry

One of the coolest results that came out of this work was the power of interferometry and photometry together. With tools like jaxoplanet/starry, which use the spherical harmonics to model rotational light curves, we can see the information gained by combining interferometry and photometry. We found that interferometry with arrays like CHARA lack information about the broadest spatial details of the star, the lowest order spherical harmonics. But photometry does really well at probing information on these modes, especially high-precision photometry from space telescopes like TESS! By combining these together, we can get nearly an order of magnitude improvement in the precision of the surface map.

I’m Shashank! I’m a third year PhD candidate in astrophysics at University of Queensland in Brisbane, Australia. I also enjoy photography and play badminton.

Wrong guy? You might be looking for him

My life and education

Here’s where I post what I’ve been up to lately. These are sometimes but not always research updates. Other things I post about include things I’ve been working on for fun, personal project interests, musings and other things I think might be helpful to share.

What is interferometry?

For a long time I’ve been meaning to use this blog as a way of explaining my ongoing research interests to my friends who may or may not be astronomers. As I’m coming up on my first-year PhD confirmation, I’m reflecting on everything I’ve learned in the past year. As a way of procrastinating writing my confirmation report, I thought I’d sit down and write up an explanation of the technique I have been learning for much of my PhD so far: interferometry. Perhaps the visuals I’ve made may come in handy for my confirmation too.

A 3d-printed moon nightlight

I’ve been continuing to put my 3d printer through its paces recently, and found out about an intruiging use for 3d printers: printing lithophanes. Lithophanes are objects made from translucent material where the thickness is modulated to produce an image when backlit. One of the most interesting such prints I found was a spherical moon lithophane–which begged me to design and make a nightlamp surrounding it.

A foldable model of JWST

I’ve been very excited for the launch of the James Webb Space Telescope (JWST) for a long time. So long, in fact, that I’ve had a JWST poster up in my bedroom since about 2012 or 2013, when I was 12 years old.

Hello world

Hello everyone! This is the intro post for my blog, which I intend to use for semi regular research updates, musings, and side projects which I always seem to be working on. For my main research projects, check out the research porfolio on my home page.

You can email me at:

Or, you can find me on Twitter at AstroShashank or Bluesky at astroshashank.bsky.social!

My research focuses on developing techniques to map the surfaces and structures of stars and exoplanets. Recently, I have been building analytic, differentiable models for photometric, spectroscopic, and interferometric observations, and working towards a suite of open-source JAX software packages [1, 2, 3, 4] implementing them. I apply these models to high-precision data from instruments such as JWST and CHARA to create detailed surface maps and to investigate how rotation and tides deform stars and planets.